一、命题原则
本课程主要教授数理逻辑、集合论、代数系统、图论方面的基础知识,是计算机科学教学中一些后续课程学习的基础和工具。通过本课程的学习,要使学生掌握离散数学的基本概念和基本原理,以现代数学的观点和方法,初步掌握处理离散结构所必须的描述工具和方法。同时,也要培养学生抽象思维、缜密概括、逻辑推理的能力,从而使学生具有良好的开拓专业理论的素质和使用所学知识,分析和解决实际问题的能力。命题以课程教学大纲和教材为依据,考查学生对基本概念、基本结论和基本方法的理解和应用,难题:中等难题:简单题的比例依次为1:4:5。
二、考试形式与成绩评定
期末考试方式为闭卷、笔试,试卷满分为100分,考试时间为120分钟。
三、考查内容和基本要求
第一章 命题逻辑
1、考试内容
命题、命题联结词、永真公式、范式、推理理论
2、考试要求
(1)理解命题和逻辑联结词的基本概念;
(2)掌握公式分类和真值表构造。
(3)理解命题等值关系式;
(4)掌握公式的析取范式和合取范式;
(5)掌握重要的重言蕴涵式;
(6)理解推理的形式结构
第二章 一阶逻辑
1、考试内容
谓词、量词、量词的辖域、永真式、改名规则、推理规则
2、考试要求
(1)掌握一阶逻辑的命题符号化;
(2)理解谓词公式与解释。
(3)掌握一阶逻辑的等值关系式;
(4)掌握一阶逻辑的推理理论。
第三章 集合
1、考试内容
集合的定义、性质、容斥原理、笛卡尔积
2、考试要求
(1)了解集合的基本概念;
(2)理解集合的运算和性质;
(3)掌握集合的笛卡尔乘积
(4)掌握笛卡尔乘积的性质
第四章 二元关系
1、考试内容
关系的定义、二元关系的性质、关系的运算、等价关系、偏序关系
2、考试要求
(1)理解二元关系的概念;
(2)掌握二元关系的运算和性质;
(3)了解关系的闭包;
(4)掌握等价关系和划分;
(5)掌握偏序关系和最值极值的判断。
第七章 代数系统
1、考试内容
代数、代数的运算性质、同构
2、考试要求
(1)掌握二元运算及其性质;
(2)掌握代数系统的概念。
(3)了解同态与同构的基本概念
第八章 半群与群
1、考试内容
群的定义、群、循环群
2、考试要求
(1)理解群的定义与性质;
(2)了解子群的概念和判别方法;
(4)掌握循环群的判断。
第十章 格与布尔代数
1、考试内容
格、格的性质、布尔代数
2、考试要求
(1)了解格和布尔代数的基本概念;
(2)理解格的定义和性质;
(3)掌握分配格、有补格、布尔代数性质。
第十一章 图
1、考试内容
图的基本概念、图的连通性、矩阵表示和运算、特殊图
2、考试要求
(1)理解图的基本概念
(2)理解图的联通性
(3)掌握图的矩阵表示
(4)掌握特殊图的性质与应用
四、题型、题量与分值
1、试卷题型比例
序号 |
题型 |
分数分配 |
题量 |
1 |
选择题 |
20 |
5-10 |
2 |
填空题 |
20 |
3-5 |
3 |
计算题 |
40 |
3-5 |
4 |
证明题 |
20 |
1-2 |
2、章节分值分配
章节 |
内容 |
大概分数分配 |
1 |
命题逻辑 |
15 |
2 |
一阶逻辑 |
15 |
3 |
集合 |
5 |
4 |
二元关系 |
30 |
5 |
代数系统 |
15 |
6 |
格与布尔代数 |
5 |
7 |
图 |
15 |
五、参考教材
《离散数学》,刘玉珍主编,武汉大学出版社,第二版,2015 年;
附1 ylzzcom永利总站线路检测《离散数学》试卷样卷
格式要求:宋体小4号,单倍行距,A4纸型
一、选择题(每题2分,共20分)
1.设有集合
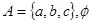 为空集,则下列 是正确的。
为空集,则下列 是正确的。
A.
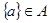 B.
B.
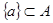 C.
C.
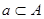 D.
D.
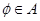
二、填空题(每空2分,共20分)
1.命题公式
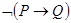 的特异析取范式为 ,特异合取范式为 。
的特异析取范式为 ,特异合取范式为 。
三、计算题(每题8分,共40分)
1.设
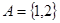 ,
,
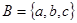 ,试求
,试求
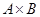 ,
,
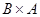 ,
,
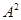 ,
,
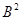 。
。
四、证明题(每题10分,共20分)
1.试证明
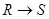 是
是
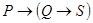 ,
,
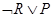 ,
,
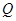 的结论。
的结论。