一、基本信息
课程名称：高等数学
课程类别：基础课
学时：82学时/64学时/54学时
二、内容简介
高等数学是药学类、管理类、人文类、检验类各专业的一门基础课。它的目的和任务是使学生系统地获得微积分、向量代数、空间解析集合几何、常微分方程的基本知识，掌握基本概念、基本理论、基本运算和方法。注意培养学生的抽象思维、逻辑思维的能力，还适当进行分析、判断和解答问题的初步训练。通过本课程的教学为后继课程如物理、化学、生物化学、数理统计、药代动力学等奠定必要的数学基础。同时也为学生今后从事科研工作提供一些有关的数学知识。
三、各章节教学目的要求和内容
第一章 函数与极限
【目的要求】
1.了解函数概念及相关性质。
2.熟悉数列与函数极限的概念。
3.掌握数列与函数极限的计算方法。
【教学内容】
1.理解函数的概念及函数的奇偶性、单调性、周期性和有界性。
2.理解复合函数和反函数的概念。
3.熟悉基本初等函数的性质及其图形。
4.会建立简单实际问题中的函数关系式。
5.理解极限的概念(对极限的
、
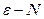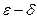定义可在学习过程中逐步加深理解，对于给出
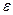求N或
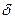不作过高的要求。)，掌握极限四则运算法则。
6.了解无穷小、无穷大以及无穷小的阶的概念。会用等价无穷小求极限。
7.理解极限存在的夹逼准则，了解单调有界准则，会用两个重要极限求极限。
8.理解函数在一点连续和在一个区间上连续的概念，了解间断点的概念，并会判别间断点的类型。
9.了解初等函数的连续性和闭区间上连续函数的性质(介值定理和最大、最小值定理)。
【教学方法】
课堂讲授
【教学时数】
10学时
第二章 导数与微分
【目的要求】
了解：导数和微分的概念。
熟悉：导数的求导法则和基本初等函数的导数公式。
掌握：函数一阶、二阶导数的求法
【教学内容】
1.理解导数和微分的概念，能用导数描述一些物理量，了解函数可导与连续的关系；
2.熟悉导数和微分的运算法则，导数的基本公式，能熟练计算初等函数的一、二阶导数；
3.会求隐函数的导数，会求参数方程的导数和二阶导数。
【教学方法】
课堂讲授
【教学时数】
8学时
第三章 导数的应用
【目的要求】
熟悉：中值定理的内容。
掌握：用中值定理证明一些简单的题目。
掌握：用洛必达(L’Hospital)法则计算函数的极限。
掌握：用导数研究函数的性态。
【教学内容】
1.理解罗尔、拉格朗日定理，会应用罗尔定理和拉格朗日定理证明一些简单问题；
2.会用洛必达(L’Hospital)法则求不定式的极限。
3.理解函数的极值概念，掌握用导数判断函数的单调性和求极值的方法。会求解较简单的最大值和最小值的应用问题。
4.会用导数判断函数图形的凹凸性，会求拐点，会描绘函数的图形(包括水平和铅直渐进线)。
【教学方法】
课堂讲授
【教学时数】
8学时
第四章 不定积分
【目的要求】
了解：不定积分的概念。
熟悉：不定积分的性质。
掌握：不定积分的基本公式、换元法和分部积分法。
【教学内容】
1.理解原函数与不定积分的概念及性质。
2.悉不定积分基本公式，熟练掌握不定积分、定积分的换元法，分部积分法；掌握简单的有理函数积分。
【教学方法】
课堂讲授
【教学时数】
6学时
第五章 定积分及其应用
【目的要求】
了解：定积分和广义积分的概念
熟悉：定积分的性质和牛顿—莱布尼兹公式。
掌握：定积分和广义积分的换元法和分部积分法。
【教学内容】
1.理解定积分的概念及性质，了解可积条件。会求简单的有理函数的积分。
2.理解变上限的积分作为其上限的函数及其求导定理，掌握牛顿—莱布尼兹公式。
3.掌握定积分的换元法和分部积分法。
4.解广义积分的概念以及广义积分的换元法和分部积分法。
5.熟练掌握用定积分表达一些物理量（如面积、体积、弧长、压力、功、引力等）的方法。
【教学方法】
课堂讲授
【教学时数】
8学时
第六章 空间解析几何
【目的要求】
了解：向量概念；
掌握：向量运算，两向量夹角的求法与两向量垂直与平行的条件。
熟悉：平面方程和直线方程的求法及
了解：曲面方程的概念，常用二次曲面的方程及其图形
了解：空间曲线的参数方程和一般方程。
【教学内容】
1.理解向量概念；
2.掌握向量运算，两向量夹角的求法与两向量垂直与平行的条件；
3.熟悉平面方程和直线方程的求法。
4.解曲面方程的概念，掌握常用的二次曲面的方程及其图形，掌握坐标轴为旋转轴的旋转曲面及母线平行坐标轴的柱面方程；
5.知道空间曲线的参数方程和一般方程。
【教学方法】
课堂讲授
【教学时数】
4学时
第七章 多元函数微分学
【目的要求】
了解：多元函数的概念及多元函数的极限和连续性。
熟悉：偏导数和全微分的定义。
掌握：多元函数与隐函数的微分法。
【教学内容】
1.理解多元函数概念；
2.理解偏导数、全微分的概念；
3.了解方向导数和梯度概念，并掌握它们的计算方法。
4.熟练掌握复合函数微分法，会求二阶偏导数；
5.会求隐函数的导数；
6.理解多元函数极值的概念，会求函数的极值。了解条件极值的概念；会求一些简单的最大、最小值问题。
【教学方法】
课堂讲授
【教学时数】
10学时
第八章 多元函数积分学
【目的要求】
了解：二重积分的概念及简单性质。
掌握：二重积分、对坐标的曲线积分的计算。
熟悉：格林公式
【教学内容】
1.理解二重积分，三重积分的概念，知道积分的性质；
2.熟练掌握二重积分的计算方法，（直角坐标、极坐标）；
3.了解对坐标的曲线积分的概念及性质；
4.掌握对坐标的曲线积分的计算方法；
5.熟悉格林公式，会运用平面曲线积分与路经无关的条件
【教学方法】
课堂讲授
【教学时数】
10学时
第九章 微分方程
【目的要求】
了解：微分方程的概念。
掌握：几种常见一阶微分方程的解法。
熟悉：二阶常系数（齐次）线性微分方程的解法；
熟悉：拉普拉斯变换解微分方程。
【教学内容】
1.了解微分方程、解、通解、特解和初始条件的概念；
2.会识别下列几种一阶微分方程：可分离变量方程、齐次方程、一阶线性方程。
3.熟练掌握可分离变量方程及一阶线性方程的解法；
4.知道下列几种特殊的高阶方程；
5.了解二阶线性方程解的结构；
6.熟练掌握二阶常系数齐次线性微分方程的解法；
【教学方法】
课堂讲授
【教学时数】
8学时
